字符串算法与哈希技巧

By Niolle

Hash

Hash 定义

我们定义一个把字符串映射到整数的函数 $f$,这个 $f$ 称为 Hash 函数 我们希望这个函数 $f$ 可以方便地帮我们判断两个字符串是否相等 Hash 的核心思想在于，将输入映射到一个值域较小、可以方便比较的范围

性质

具体来说，哈希函数最重要的性质可以概括为下面两条：

在 Hash 函数值不一样的时候，两个字符串一定不一样； 在 Hash 函数值一样的时候，两个字符串不一定一样（但有大概率一样，且我们当然希望它们总是一样的）。 我们将 Hash 函数值一样但原字符串不一样的现象称为哈希冲突。

基本形式

通常我们采用的是多项式 Hash 的方法，对于一个长度为 l 的字符串 $s$ 来说，我们可以这样定义多项式 Hash 函数

$$f(s)=\sum _{i=1}^{l}s[i]\times b^{l-i}(\mathrm{mod}M)$$

例如，对于字符串 $xyz$，其哈希函数值为 $x{b}^2+yb+z$

其中M为哈希模数,我们习惯取一个大质数,如${10}^9+7,998244353$

Hash Code

int M = 1e9 + 7;
int B = 233;
using ll = long long;
int get_hash(string s) {
  int res = 0;
  for (int i = 0; i < s.size(); ++i) {
    res = (1ll * res * B + s[i]) % M; //过程中会超出int范围,故×1ll
  }
  return res;
}
bool cmp(string s,string t) {
  return get_hash(s) == get_hash(t);
}

处理哈希冲突

• 多值哈希

  多值 Hash,就是有多个 Hash 函数，每个 Hash 函数的模数不一样，这样就能解决 Hash 冲突的问题。

  判断时只要有其中一个的 Hash 值不同，就认为两个字符串不同，若 Hash 值都相同，则认为两个字符串相同。

  一般来说，双值 Hash 就够用了。

双值Hash Code

int M = 1e9 + 7, m = 998244353;
int B = 233;
using ll = long long;
int get_hash1(string s) {
  int res = 0;
  for (int i = 0; i < s.size(); ++i) {
    res = (1ll * res * B + s[i]) % M; //过程中会超出int范围,故 × 1ll
  }
  return res;
}
int get_hash2(string s) {
  int res = 0;
  for (int i = 0; i < s.size(); ++i) {
    res = (1ll * res * B + s[i]) % m; //过程中会超出int范围,故 × 1ll
  }
  return res;
}
bool cmp(string s,string t) {
  if(get_hash1(s) != get_hash1(t)) return 0;
  if(get_hash2(s) != get_hash2(t)) return 0;
  return 1;
}

处理哈希冲突

• 大模数哈希

• 依据1e9级别模数冲突原理——生日攻击理论,比较次数只要达到 级别就有超过50%的概率发生crash.这种写法被卡掉的根本原因是概率不对. 采取1e18级别的质数作为模数即可,如${10}^{18}+3$ 注意乘法过程中要开__int128

luogu P3370 【模板】字符串哈希

如题，给定 N 个字符串（第 i 个字符串长度为 $M_i$, 字符串内包含数字、大小写字母，大小写敏感），请求出 N 个字符串中共有多少个不同的字符串。

对于 $100$ 的数据：$N\le 10000，M_i\approx 1000，M_{max}\le 1500$

题解

• 模板题，对于每个字符串求出他的哈希值，再$n^2$暴力比较即可

luogu P3805 【模板】manacher

给出一个只由小写英文字符 $a,b,c,\dots ,y,z$ 组成的字符串 S ,求 S 中最长回文串的长度 。字符串长度为 n。

对于 $100$ 的数据：$N\le 10000，M_i\approx 1000，M_{max}\le 1500$

题解

马拉车板子，但是也有个很经典的哈希做法，即二分+Hash 如何判断字符串是否是哈希呢？只需要某个区间正着的Hash值和反着的Hash值相同

//判断是否为回文串
bool check(string s) {
  string t = ReverseString(s); //t是s的翻转串
  return get_hash(s) == get_hash(t);
}

通常需要判断的是某个区间是否为回文串，使用substr()再跑hash会很慢，这里介绍使用前缀和作差得到区间Hash值的方法

设$hash[i]$表示字符串S前i个字符的Hash值，$hash[i]=(hash[i-1]\ast B+s[i])\mathrm{mod}M$则区间$[l,r]$的Hash值就是$hash[r]-hash[l-1]\ast b^{r-(l-1)}(\mathrm{mod}M)$

判断一个区间是否为回文串可以使用这个区间正着的Hash值是否等于这个区间反着的Hash着来判断

这个区间反着的Hash值具体求法为，设rhash[i]表示字符串S后i个字符的Hash值，$rhash[i]=(rhash[i+1]\ast B+s[i])\mathrm{mod}M$，则区间$[l,r]$的反着的Hash值就是r$hash[l]-hash[r+1]\ast b^{r-(l-1)}(\mathrm{mod}M)$

回到原问题，如何找到最长的最长回文串

直接枚举子区间判断是否为回文串可做到O(n^2)的复杂度 二分的解法为，先枚举对称中心，然后二分每个对称中心的最长回文串长度，这个是存在单调性的，即若区间$[i-k,i+k]$是回文串，则$[i-(k-1),i+(k-1)]$也一定是回文串，二分这个长度即可，用Hash判断其是否为回文串。

时间复杂度：$O(n\log n)$

---

KMP

border定义

border ：若字符串 $s$ 存在某个真前缀和某个真后缀相同，则这个真前缀或真后缀称为 的一个 border。一个字符串的Border可能有多个。

前缀函数定义

给定一个长度为 n 的字符串 s，其 前缀函数 被定义为一个长度为 n 的数组 $\pi$。 其中 $\pi [i]$ 的定义是：

1.如果子串 $s[0\dots i]$ 有一对相等的真前缀与真后缀：$s[0\dots k-1]$ 和 $s[i-(k-1)\dots i]$，那么 $\pi [i]$ 就是这个相等的真前缀（或者真后缀，因为它们相等）的长度，也就是 $\pi [i]=k$; 2.如果不止有一对相等的，那么 $\pi [i]$ 就是其中最长的那一对的长度； 3.如果没有相等的，那么 \pi[i]=0。 简单来说 $\pi [i]$ 就是，子串 $s[0\dots i]$ 最长的相等的真前缀与真后缀的长度。 特别地，规定 $\pi [0]=0$。 前缀函数有一种简单的定义，就是最长的Border

前缀函数求解过程

过程 举例来说，对于字符串 abcabcd，

$\pi [0]=0$，因为 a 没有真前缀和真后缀，根据规定为 0 $\pi [1]=0$，因为 ab 无相等的真前缀和真后缀 $\pi [2]=0$，因为 abc 无相等的真前缀和真后缀 $\pi [3]=1$，因为 abca 只有一对相等的真前缀和真后缀：a，长度为 1 $\pi [4]=2$，因为 abcab 相等的真前缀和真后缀只有 ab，长度为 2 $\pi [5]=3$，因为 abcabc 相等的真前缀和真后缀只有 abc，长度为 3 $\pi [6]=0$，因为 abcabcd 无相等的真前缀和真后缀

同理可以计算字符串 aabaaab 的前缀函数为 [0, 1, 0, 1, 2, 2, 3]。

计算前缀函数的朴素做法

一个直接按照定义计算前缀函数的算法流程：

在一个循环中以 $i=1\to n-1$ 的顺序计算前缀函数 $\pi [i]$ 的值（$\pi [0]$ 被赋值为 0） 为了计算当前的前缀函数值 $\pi [i]$，我们令变量 $j$ 从最大的真前缀长度 $i$ 开始尝试。 如果当前长度下真前缀和真后缀相等，则此时长度为 $\pi [i]$，否则令 $j$ 自减 1，继续匹配，直到 $j=0$。 如果 $j=0$ 并且仍没有任何一次匹配，则置 $\pi [i]=0$ 并移至下一个下标 $i+1$。 显见该算法的时间复杂度为 $O(n^3)$，具有很大的改进空间。

第一个优化

第一个重要的观察是 相邻的前缀函数值至多增加 1。

参照下图所示，只需如此考虑：当取一个尽可能大的 $\pi [i+1]$ 时，必然要求新增的 $s[i+1]$ 也与之对应的字符匹配，即 $s[i+1]=s[\pi [i]]$, 此时 $\pi [i+1]=\pi [i]+1$

$\underset{\pi [i+1]=4}{\underbrace{\stackrel{\pi [i]=3}{\overbrace{s_0{s}_1{s}_2}}{s}_3}}\dots \underset{\pi [i+1]=4}{\underbrace{\stackrel{\pi [i]=3}{\overbrace{s_{i-2}{s}_{i-1}{s}_i}}{s}_{i+1}}}$ 所以当移动到下一个位置时，前缀函数的值要么增加一，要么维持不变，要么减少。 加上这个优化可以将复杂度均摊到$O(n^2)$，因为不用暴力枚举所有可能的前缀，只需要从$\pi [i-1]+1$开始枚举即可 而且如果当前$p[i]=k$,则$$

Code

vector<int> prefix_function(string s) {
  int n = (int)s.length();
  vector<int> pi(n);
  for (int i = 1; i < n; i++)
    for (int j = pi[i - 1] + 1; j >= 0; j--)  // improved: j=i => j=pi[i-1]+1
      if (s.substr(0, j) == s.substr(i - j + 1, j)) {
        pi[i] = j;
        break;
      }
  return pi;
}

第二个优化

在第一个优化中，我们讨论了计算 $\pi [i+1]$ 时的最好情况：$s[i+1]=s[\pi [i]]$，此时 $\pi [i+1]=\pi [i]+1$。 现在让我们沿着这个思路走得更远一点：讨论当 $s[i+1]\ne s[\pi [i]]$ 时如何跳转。 失配时，我们希望找到对于子串 $s[0\dots i]$，仅次于 $\pi [i]$ 的第二长度 $j$，使得在位置 i 的前缀性质仍得以保持，也即 $s[0\dots j-1]=s[i-j+1\dots i],j=\pi [\pi [i]-1]：$$\stackrel{\pi [i]}{\overbrace{\underset{j}{\underbrace{s_0{s}_1}}{s}_2{s}_3}}\dots \stackrel{\pi [i]}{\overbrace{s_{i-3}{s}_{i-2}\underset{j}{\underbrace{s_{i-1}{s}_i}}}}{s}_{i+1}$ 如果我们找到了这样的长度 j，那么仅需要再次比较 $s[i+1]$ 和 $s[j]$。如果它们相等，那么就有 $\pi [i+1]=j+1$。否则，我们需要找到子串 $s[0\dots i]$ 仅次于 j 的第二长度 $j^{(2)}=\pi [j-1]$，使得前缀性质得以保持，如此反复，直到 $j=0$。如果 $s[i+1]\ne s[0]$，则 $\pi [i+1]=0$。

KMP Code

显然我们可以得到一个关于 j 的状态转移方程：

$$j^{(n)}=\pi [j^{(n-1)}-1],(j^{(n-1)}>0)$$

结合上述的两个优化，可以得到时间复杂度为$O(n)$的求解前缀函数的做法，即KMP算法

vector<int> prefix_function(string s) {
  int n = (int)s.length();
  vector<int> pi(n);
  for (int i = 1; i < n; i++) {
    int j = pi[i - 1];
    while (j > 0 && s[i] != s[j]) j = pi[j - 1];
    if (s[i] == s[j]) j++;
    pi[i] = j;
  }
  return pi;
}

border性质

border ：若字符串 $s$ 存在某个真前缀和某个真后缀相同，则这个真前缀或真后缀称为 的一个 border。一个字符串的Border可能有多个。

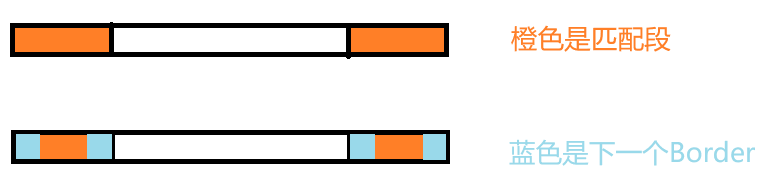
• 性质1:对于任意一个字符串S,一个Border的长度就对应一个Border(比如abcdabc的长度为3的Border当然就只能是abc)。并且,假设S长度记为n,则S的则S所有Border长度分别为:$\pi [n-1],\pi [\pi [n-1]-1],\pi [\pi [\pi [n-1]-1]-1]$
• 性质2：根据该结论，求出$\pi$函数即可得到整个字符串的所有border

性质图示

在字符串中查找子串(luogu KMP模板题)

给定一个文本 $t$ 和一个字符串 s，我们尝试找到并展示 s 在 t 中的所有出现。

为了简便起见，我们用 n 表示字符串 s 的长度，用 m 表示文本 t 的长度。

我们构造一个字符串 $\text{s + \#\# + t}$，其中 $\mathrm{\#}$ 为一个既不出现在 s 中也不出现在 t 中的分隔符。接下来计算该字符串的前缀函数。现在考虑该前缀函数除去最开始 n + 1 个值（即属于字符串 s 和分隔符的函数值）后其余函数值的意义。根据定义，$\pi [i]$ 为右端点在 i 且同时为一个前缀的最长真子串的长度，具体到我们的这种情况下，其值为与 s 的前缀相同且右端点位于 i 的最长子串的长度。由于分隔符的存在，该长度不可能超过 n。而如果等式 $\pi [i]=n$ 成立，则意味着 s 完整出现在该位置（即其右端点位于位置 i）。注意该位置的下标是对字符串 $\text{s + \#\# + t}$ 而言的。 时间复杂度：$O(n+m)$

Code

vector<int> find_occurrences(string text, string pattern) {
  string cur = pattern + '#' + text;
  int sz1 = text.size(), sz2 = pattern.size();
  vector<int> v;
  vector<int> lps = prefix_function(cur);
  for (int i = sz2 + 1; i <= sz1 + sz2; i++) {
    if (lps[i] == sz2) v.push_back(i - 2 * sz2);
  }
  return v;
}

字符串的周期

对字符串 $s$ 和 $0<p\le |s|$，若 $s[i]=s[i+p]$ 对所有 $i\in [0,|s|-p-1]$ 成立，则称 p 是 s 的周期。

对字符串 $s$ 和 $0\le r<|s|$，若 $s$ 长度为 $r$ 的前缀和长度为 r 的后缀相等，就称 s 长度为 r 的前缀是 s 的 border。

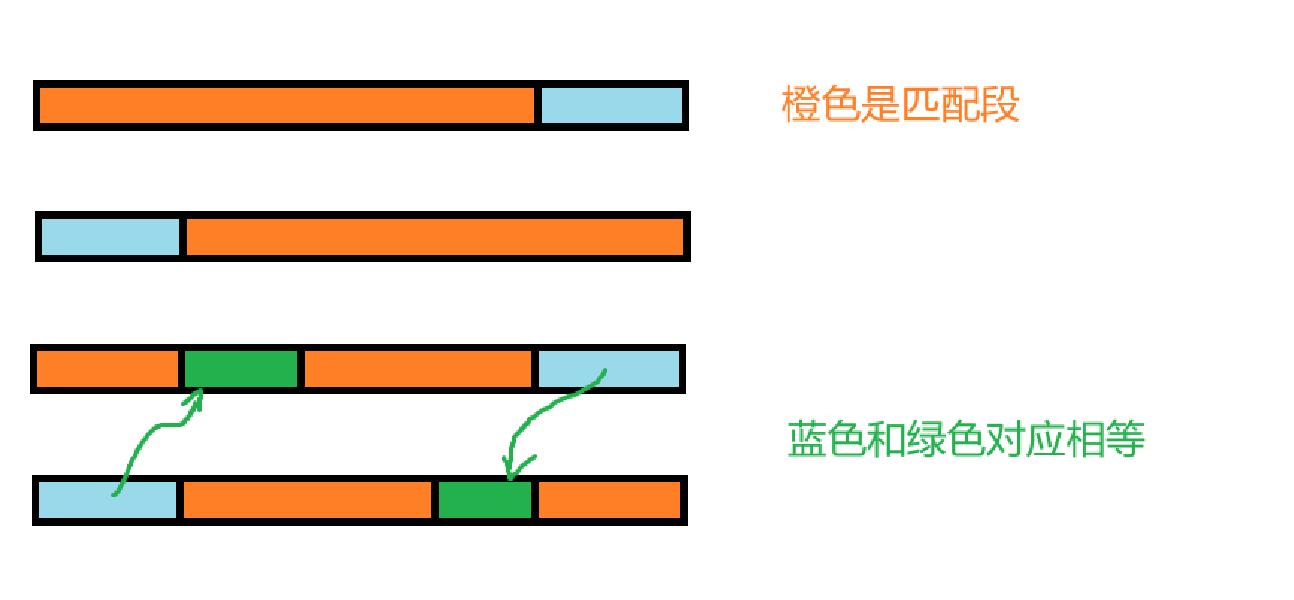
由 s 有长度为 r 的 border 可以推导出 $|s|-r$ 是 s 的周期。

根据前缀函数的定义，可以得到 s 所有的 border 长度，即 $\pi [n-1],\pi [\pi [n-1]-1],\dots$

所以根据前缀函数可以在 O(n) 的时间内计算出 s 所有的周期。其中，由于 \pi[n-1] 是 s 最长 border 的长度，所以 $n-\pi [n-1]$ 是 s 的最小周期。

图示

统计每个前缀的出现次数

给定一个长度为 n 的字符串 s，我们希望统计每个前缀 $s[0\dots i]$ 再字符串 s 中的出现次数。

首先让我们来解决第一个问题。考虑位置 $i$ 的前缀函数值 $\pi [i]$。根据定义，其意味着字符串 $s$ 一个长度为 $\pi [i]$ 的前缀在位置 $i$ 出现并以 $i$ 为右端点，同时不存在一个更长的前缀满足前述定义。与此同时，更短的前缀可能以该位置为右端点。容易看出，我们遇到了在计算前缀函数时已经回答过的问题：给定一个长度为 j 的前缀，同时其也是一个右端点位于 i 的后缀，下一个更小的前缀长度 k < j 是多少？该长度的前缀需同时也是一个右端点为 i 的后缀。因此以位置 i 为右端点，有长度为 $\pi [i]$ 的前缀，有长度为 $\pi [\pi [i]-1]$ 的前缀，有长度为 $\pi [\pi [\pi [i]-1]-1]$ 的前缀，等等，直到长度变为 0。故而我们可以通过下述方式计算答案。

Code

vector<int> ans(n + 1);
for (int i = 0; i < n; i++) ans[pi[i]]++;
for (int i = n - 1; i > 0; i--) ans[pi[i - 1]] += ans[i];
for (int i = 0; i <= n; i++) ans[i]++;

一个字符串中本质不同子串的数目

给定一个长度为 n 的字符串 s，我们希望计算其本质不同子串的数目。

我们将迭代的解决该问题。换句话说，在知道了当前的本质不同子串的数目的情况下，我们要找出一种在 s 末尾添加一个字符后重新计算该数目的方法。

令 k 为当前 s 的本质不同子串数量。我们添加一个新的字符 c 至 s。显然，会有一些新的子串以字符 c 结尾。我们希望对这些以该字符结尾且我们之前未曾遇到的子串计数。

构造字符串 $t=s+c$ 并将其反转得到字符串 $t^{\sim }$。现在我们的任务变为计算有多少 $t^{\sim }$ 的前缀未在 $t^{\sim }$ 的其余任何地方出现。如果我们计算了 $t^{\sim }$ 的前缀函数最大值 ${\pi }_{max}$，那么最长的出现在 s 中的前缀其长度为 ${\pi }_{max}$。自然的，所有更短的前缀也出现了。

因此，当添加了一个新字符后新出现的子串数目为 $|s|+1-{\pi }_{max}$。 最终复杂度为 $O(n^2)$。

推荐习题

https://loj.ac/d/588

字符串的第一章和第二章